[논문리뷰] Fixed-point Inversion for Text-to-image diffusion models

Fixed-point Inversion for Text-to-image diffusion models
https://arxiv.org/abs/2312.12540

요약: DDIM Inversion에서 각 스텝마다 인버전을 위해 linearity를 가정하고 뒤로 가는 노이즈를 forward noise로부터 근사를 하는데, 각 스텝마다 근사 에러가 누적되어 결과가 정확하지 않다. 이를 해결하기 위해 근사가 도입되기 전의 DDIM inversion 식을 implicit function 꼴로 만들고, implicit function을 풀 때 일반적으로 사용하는 수치해석기법인 fixed-point iteration을 통해 해를 구하면 훨씬 정확한 인버전이 가능하다!

DDIM inversion의 선형 근사. 그림은 ReNoise: Real Image Inversion Through Iterative Noising에서 가져옴

 

이번엔 ChatGPT를 활용해 번역해 봤는데 결과가 꽤 좋다. 프롬프트를 조금만 더 갈고닦으면 훌륭한 퀄리티로 번역할 수 있을 것 같다.

Abstract

텍스트 가이드 디퓨전 모델(diffusion model)은 이미지를 생성하고 조작하는 새로운 강력한 방법을 제공합니다. 이러한 모델의 여러 응용 프로그램에는 이미지 편집, 보간(interpolation), 의미적 증강(semantic augmentation)이 포함되며, 이들은 디퓨전 인버전(inversion)이 필요합니다. 이는 주어진 이미지를 생성할 수 있는 노이즈 시드를 찾는 과정입니다. 현재 주어진 이미지를 인버전하는 기술은 느리거나 부정확할 수 있습니다. 디퓨전 과정을 인버전하는 기술적 도전은 잠재적인 변수(latent)에 대한 암시적 방정식(implicit equation)에서 비롯되며, 이는 폐쇄형으로 해결할 수 없습니다. 이전 접근법에서는 이 문제를 근사치나 다양한 학습 체계(learning schemes)를 사용하여 해결하려고 제안했습니다. 여기서, 우리는 문제를 고정점(fixed point) 방정식 문제로 정식화하고 수치 해석(numerical analysis)에서 잘 연구된 접근법인 고정점 반복(fixed-point iterations)을 사용하여 해결합니다. 또한, 우리는 실제 이미지의 잠재 공간(latent space)으로 인코딩될 때 크게 영향을 미치는 일관성 없는 원인을 확인합니다. 우리는 인코딩을 프롬프트 인식(prompt-aware) 조정을 적용하여 수정하는 방법을 보여줍니다. 우리의 해결책인 고정점 인버전(Fixed-point inversion)은 EDICT와 Null-text와 같은 이전 기술보다 훨씬 빠르며, 비슷한 인버전 품질을 제공합니다. 이는 어떤 사전 훈련된 디퓨전 모델과 결합될 수 있으며 모델 훈련, 프롬프트 튜닝, 추가 파라미터가 필요 없습니다. 일련의 실험에서, 고정점 인버전은 여러 하류 작업(downstream tasks)에서 개선된 결과를 보여줍니다: 이미지 편집, 이미지 보간, 그리고 희귀한 객체의 생성.

 

1. Introduction

텍스트-이미지 디퓨전 모델은 사용자가 제공한 텍스트 프롬프트를 바탕으로 다양하고 고해상도의 이미지를 생성할 수 있습니다. 이러한 모델은 초기 노이즈(시드)를 발견하는 등, 인버전이 필요한 여러 중요한 작업에 추가적으로 사용됩니다. 이 시드는 프롬프트와 함께 전진(디노이징) 디퓨전 과정을 거쳐 입력 이미지를 생성합니다. 인버전은 이미지 편집, 개인화, 시드 노이즈 보간 및 희귀 개념 생성과 같은 다양한 작업에 사용됩니다. 인버전은 여러 작업의 중요한 인프라 구성 요소가 되면서 여러 인버전 방법이 개발되었습니다. 주로, Denoising Diffusion Implicit Models (DDIM)은 초기 노이즈 시드를 생성된 이미지로 매핑하는 결정론적 샘플링 기술을 도입했습니다. 반대로, DDIM 인버전은 이 기술을 사용하여 이미지를 latent 노이즈 표현으로 변환하며, 인버전 방정식을 근사화합니다. 이 근사화는 매우 빠르지만(단일 A100 GPU에서 약 1.5초), 일관성 없는 결과를 초래하여 생성된 이미지에 눈에 띄는 영향을 줍니다. DDIM 인버전의 이러한 일관성 없는 문제를 해결하기 위한 여러 시도가 이미 이루어졌습니다. Null-text는 인버전 과정과 생성 과정의 디퓨전 상태를 조정함으로써 가깝게 만들고자 합니다. EDICT는 두 개의 결합된 노이즈 벡터를 사용하여 번갈아 가며 서로를 인버전하고, 정확한 디퓨전 인버전에 도달합니다. Null-text와 EDICT 모두 높은 품질의 재구성 결과를 제공하지만, 훨씬 더 높은 계산 비용이 필요합니다: 각 인버전된 이미지에 대해 각각 3M 또는 16K 파라미터를 저장하고, 인버전 당 20초 또는 60초가 소요됩니다. 이는 DDIM 인버전보다 훨씬 느립니다.

이 논문에서는 빠르고 간단하며 충실도를 보존하는 절차를 사용하여 인버전의 일관성 문제를 다룹니다. 방정식의 수치적 해결 기법에서 출발하여, 우리는 간단한 고정점 반복 접근법을 취합니다. 우리는 이 접근법을 FPI(Fixed-Point Inversion)라고 명명합니다. FPI는 각 디퓨전 단계에서 몇 번의 고정점 반복만 적용하여 이미지의 일관된 인버전을 강제합니다. 특히, 우리는 고정점 반복 이론을 사용하여 DDIM이 도입한 암묵적 함수를 해결할 수 있음을 보여줍니다. 실제로 2~5회의 반복만으로도 수렴에 충분했으며, DDIM 인버전보다 훨씬 정확한 결과를 얻을 수 있었습니다. FPI는 모델 훈련이나 파인튜닝, 프롬프트 최적화 또는 추가 파라미터가 필요 없습니다. 모든 사전 훈련된 디퓨전 모델과 결합할 수 있습니다. 또한, 실제 이미지의 인버전을 크게 저해하는 또 다른 일관성 없는 원인을 확인했습니다. 실제 이미지가 latent 공간으로 인코딩될 때, 그 인코딩은 주어진 프롬프트에 대해 생성된 이미지를 인버전하도록 설계된 과정과 맞지 않을 수 있습니다. 우리는 인코딩의 짧은 프롬프트 인식 조정을 적용하면 FPI의 인버전 품질이 크게 향상됨을 보여줍니다. 그림 1은 FPI의 품질과 속도를 보여줍니다. FPI는 5초 이내에 실제 이미지를 인버전하며, 경쟁 방법보다 유사하거나 더 나은 품질을 달성하면서도 훨씬 빠릅니다.

2. Related Work

디퓨전 모델 인버전

텍스트-이미지 디퓨전 모델은 사용자가 제공한 텍스트 프롬프트의 지도하에 높은 차원의 공간에서 무작위 샘플(시드)을 해당 이미지로 변환합니다. DDIM은 널리 사용되는 결정론적 스케줄러로, 이미지를 그것의 latent 노이즈 시드로 인버전하는 기능을 보여줍니다. 효과적이기는 하지만, 이는 무조건적 디퓨전 모델을 위해 설계되었고, 텍스트 프롬프트나 편집을 처리할 능력이 부족했습니다. 텍스트 가이드 디퓨전 모델에 적용될 때, DDIM 인버전은 일관성이 떨어지는 문제를 겪습니다. 특히 classifier-free guidance 상수가 클 때 이러한 문제가 발생합니다. 이는 선형 근사에 의존하면서 오류의 전파가 발생하고, 이는 부정확한 이미지 재구성과 내용의 손실을 초래합니다. 최근 연구에서는 DDIM 인버전에서 발생하는 이 한계를 해결합니다. Null-text 인버전은 빈 문자열의 임베딩 벡터를 최적화하여 재구성 정확도를 개선합니다. 이는 DDIM 인버전을 사용하여 계산된 디퓨전 과정이 역 디퓨전 과정과 일치하도록 보장합니다. 또한 Null-Text 인버전 접근법을 포함시켜 빈 텍스트 임베딩을 프롬프트 임베딩으로 대체합니다. 이는 수렴 시간과 재구성 품질을 향상시키지만, 이미지 편집 품질은 떨어집니다. 이 두 연구에서, 최적화된 임베딩은 저장되어야 하며, StableDiffusion v1.5로 50번의 디노이징 단계를 거칠 때 각 이미지마다 거의 300만 개의 추가 파라미터가 필요합니다. EDICT는 특히 Affine Coupling Layers와 같은 가역 신경망 레이어를 도입하여 전후진 디퓨전 경로를 모두 계산합니다. 그러나 이는 DDIM 인버전에 비해 신경 기능 평가(NFE)의 수를 두 배로 늘리는 비용을 초래하며, 런타임을 연장시킵니다. 또한, 모든 인버전된 이미지에 대해 추가 latent가 저장되어야 합니다(StableDiffusion에서 이미지당 16K 추가 파라미터). 또 다른 제안된 접근법은 제공된 이미지와의 더 강한 연결을 확립하기 위해 노이즈 맵을 수정하는 것을 권장하며, 이는 비가우스 노이즈 분포를 결과로 합니다. 그러나 이 접근법은 계산 비용이 많이 들고, DDIM 인버전보다 10배의 시간이 필요합니다. 또한 그 적용 가능성은 오직 편집 작업에만 제한됩니다.

시드 탐색 & 희귀 개념 생성

여기에서 우리는 디퓨전 인버전(diffusion inversion)에 크게 의존하는 또 다른 태스크를 소개합니다. 일반적으로 디퓨전 모델(diffusion model)의 훈련에 사용되는 데이터는 개념의 불균형 분포를 자주 보이게 됩니다([19] 참조). 이는 디퓨전 모델이 희귀 개념의 정확한 이미지를 생성하기 어렵게 만들며, 종종 왜곡된 이미지나 밀접하게 관련되지만 다른 개념의 이미지를 생성하게 됩니다(예를 들어, "호랑이 고양이" 대신 "호랑이"를 생성함). 이러한 한계를 극복하기 위해, SeedSelect([19] 참조)는 실제 이미지와 해당 시드(seed)의 작은 세트를 사용하여 시드 최적화를 수행합니다. 이 과정은 디퓨전 모델에 의해 그럴듯한 이미지가 생성될 때까지 시드를 반복적으로 세밀하게 조정합니다. 후속 접근법인 NAO([18] 참조)는 새로운 보간 경로(NAO-path)와 시드의 중심(NAO-centroid)을 SeedSelect의 초기화를 위해 도입했습니다. NAO와 SeedSelect는 모두 초기 시드 평가를 위해 DDIM 인버전(DDIM Inversion)을 사용하며, 이는 결과에 큰 영향을 미칩니다. 현재 논문은 NAO와 SeedSelect에 대한 보다 정확한 인버전 시드를 얻기 위한 대안을 제공하여, 외형과 의미적 정확성 측면에서 더 나은 이미지를 생성하고자 합니다. 기존 인버전 기술(Null-Text([13] 참조) 및 EDICT([22] 참조))이 이 컨텍스트에서 적용할 수 없다는 점을 강조하는 것이 중요합니다. 이 기술들은 이미지 재구성을 위해 추가 파라미터가 필요하며, 이는 NAO가 제안한 보간 및 중심 식별의 직관적 구현을 방해합니다.

 

3. Method

3.1. Preliminaries

먼저 Diffusion Denoising Probabilistic Models (DDPMs)와 Denoising Diffusion Implicit Models (DDIMs)의 기본 개념을 설정합니다. 이 모델들에서 전진 단계(forward pass)는 seed noise로부터 이미지를 생성하는 과정입니다. 역단계(backward pass, 인버전(inversion))는 주어진 이미지로부터 해당하는 seed noise를 찾는 과정입니다.

Diffusion Denoising Probabilistic Models (DDPMs)

DDPMs은 데이터 샘플에 반복적으로 가우시안 노이즈를 추가함으로써 이미지를 생성하는 체계적인 과정을 학습합니다. 데이터 분포는 가우시안 분포에서 무작위 샘플(noise seed)을 시작으로 하는 역확산 과정(reverse diffusion process)을 통해 점차적으로 복원됩니다. 최근의 잠재(latent) 디퓨전 모델들에서는 이미지를 직접 다루는 대신 변분 오토인코더에서 유도된 이미지의 잠재 표현에 대해 노이징과 디노이징을 적용합니다. 특히, 노이즈로 매핑하는 과정은 $z_0$에서 시작하여 점차 노이즈를 추가함으로써 잠재 변수 $z_1, z_2, ..., z_T$를 얻는 마르코프 체인(Markov chain)으로 구성됩니다.

$$q(z_1, z_2, ..., z_T | z_0) = \prod_{t=1}^{T} q(z_t | z_{t-1})$$

각 단계는 가우시안 전이로,

$$q(z_t | z_{t-1}) := \mathcal{N}(z_t, \sqrt{1 - \beta_t} z_{t-1}, \beta_t I)$$

로 파라미터화됩니다. 여기서 $\beta_0, \beta_1, ..., \beta_T$는 (0, 1) 범위입니다. $z_t$는 $z_0$과 가우시안 노이즈 $\epsilon \sim \mathcal{N}(0, I)$의 선형 조합으로 표현될 수 있습니다.

$$z_t = \sqrt{\alpha_t} z_0 + \sqrt{1 - \alpha_t} \epsilon$$

여기서 $\alpha_t = \prod_{i=1}^{t}(1 - \beta_i)$입니다.

텍스트 가이드 디퓨전 모델(text-guided diffusion models)은 텍스트 프롬프트의 잠재 표현 $p$ (보통 CLIP 임베딩) 형태의 제어 신호로 확산 과정을 제어합니다. 디노이징 네트워크 $\epsilon_{\theta}$는 손실을 최소화하는 것을 목표로 합니다.

$$L = \mathbb{E}_{z_0, \epsilon \sim \mathcal{N}(0,1), t} [ ||\epsilon - \epsilon_{\theta}(z_t, t, p)||^2 ]$$

디노이징 네트워크 $\epsilon_{\theta}$의 역할은 각 시간 단계 $t$에서 잠재 코드 $z$에서 추가된 노이즈 $\epsilon$를 정확하게 제거하는 것이며, 이는 노이즈가 포함된 잠재 코드 $z_t$와 조절 텍스트 $p$의 인코딩을 입력으로 합니다.

Denoising Diffusion Implicit Models (DDIM)

디퓨전 모델에서 샘플링은 해당하는 확산 상미분 방정식(Ordinary Differential Equations, ODEs)을

 푸는 것으로 볼 수 있습니다. DDIM 스케줄러는 잠재 노이즈 벡터를 디노이징하는 다음 방식을 제안했습니다.

$$z_{t-1} = \sqrt{\frac{\alpha_{t-1}}{\alpha_t}} z_t - \sqrt{\alpha_{t-1}} \cdot \Delta\psi(\alpha_t) \cdot \epsilon_{\theta}(z_t, t, p)$$

여기서 $\psi(\alpha) = \sqrt{\frac{1}{\alpha} - 1}$, 그리고 $\Delta\psi(\alpha_t) = \psi(\alpha_t) - \psi(\alpha_{t-1})$ 입니다.

식 (3)에서 추가된 노이즈 항 $\epsilon$은 네트워크 $\epsilon_{\theta}(z_t, t, p)$의 출력으로 대체됩니다. 이 네트워크는 그것을 예측하기 위해 훈련되었습니다.

DDIM 인버전

이제 우리는 잠재 표현에서의 인버전에 초점을 맞춥니다. 주어진 이미지 표현 $z_0$과 해당 텍스트 프롬프트 $p$가 주어지면, 디노이즈될 때 잠재 $z_0$을 재구성하는 노이즈 시드 $z_T$를 찾습니다. 이 태스크를 위해 여러 접근법이 제안되었으며, 우리는 DDIM 인버전 기법에 집중합니다. 이 기법에서, 식 (5)는 다음과 같이 재작성됩니다:

$$z_t = \sqrt{\frac{\alpha_t}{\alpha_{t-1}}} z_{t-1} + \sqrt{\alpha_{t-1}} \cdot \Delta\psi(\alpha_t) \cdot \epsilon_{\theta}(z_t, t, p)$$ (6)

이는 $z_t$에서의 함축적 방정식이며, $z_t$를 $z_{t-1}$로 대체하여 근사할 수 있습니다:

$$\approx \sqrt{\frac{\alpha_t}{\alpha_{t-1}}} z_{t-1} + \sqrt{\alpha_{t-1}} \cdot \Delta\psi(\alpha_t) \cdot \epsilon_{\theta}(z_{t-1}, t, p)$$ (7)

근사의 품질은 $z_t - z_{t-1}$의 차이(작을수록 오류가 작음)와 $\epsilon_{\theta}$의 $z_t$에 대한 민감도에 따라 달라집니다. 자세한 내용은 [3, 21]을 참조하십시오.

식 (7)을 각 디노이징 단계 $t$마다 반복적으로 적용함으로써, 이미지의 잠재 표현 $z_0$을 시드 공간의 잠재 표현 $z_T$로 인버전할 수 있습니다. DDIM 인버전은 빠르지만, 식 (7)의 근사는 각 시간 단계마다 본질적으로 오류를 도입합니다. 이러한 오류들이 누적되면서 전체 디퓨전 과정이 전진 과정과 역진 과정에서 일관성이 없어지게 되어, 이미지 재구성과 편집의 품질이 저하됩니다.

3.2. Fixed-point Inversion

우리는 식 (7)의 근사를 대체하여 식 (6)의 암시적 방정식을 직접 해결하고자 제안합니다. 이 목적을 위해, 암시적 방정식 최적화에서 흔히 사용되는 고정점 반복 기법을 사용합니다. 특히, 반복을 나타내기 위해 상첨자 $i$를 사용하면 다음과 같습니다:

$$z^0_t = z_{t-1}$$
$$z^{i+1}_t = f(z^i_t),$$

여기서

$$f(z_t) = \sqrt{\frac{\alpha_t}{\alpha_{t-1}}} z_{t-1} + \sqrt{\alpha_{t-1}} \Delta \psi(\alpha_t) \epsilon_{\theta}(z_t, t, p).$$

즉, 주어진 $z_{t-1}$에 대해, 암시적 방정식의 잔차 오류를 최소화하기 위해 고정점 반복을 수행합니다.

 

고정점 반복?
https://jehunseo.tistory.com/118 참조
$f(x) = x$ 의 해를 수치해석적으로 찾는 방법이다. 아래 그림을 보면 직관적으로 y = f(x)에 반복적으로 값을 대입하다보면 ( $f(f(f(...f(-1)...))$ ) $y = x$와의 교점으로 수렴하는 것을 이해할 수 있다. 단 이는 특정 조건에서만 해로 수렴한다. 대표적으로 contraction mapping (미분가능한 함수일 경우 모든 점에서 기울기가 1이하인 함수) 이면 고정점 반복 결과 항상 수렴하고 해를 찾을 수 있다. 어떤 함수가 고정점을 갖는지 여부에 대한 내용은 바나흐 고정점 정리 참조.

 

고정점 반복에 대한 직관적인 이해

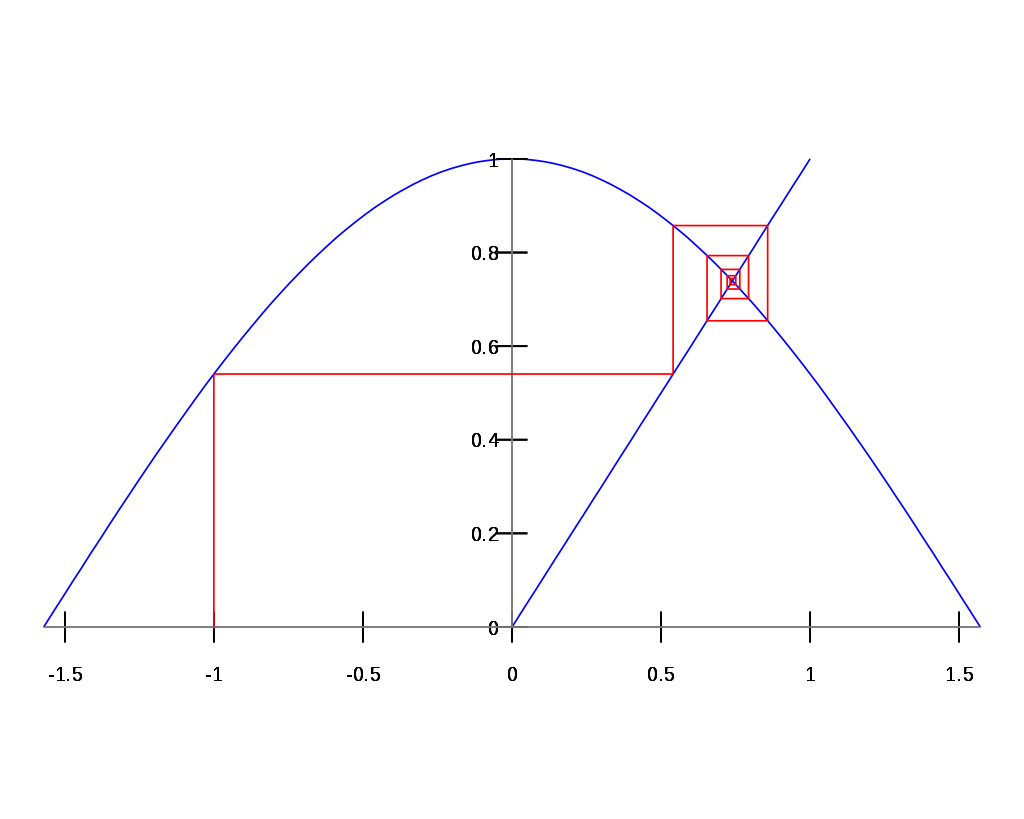
그림 2는 이 과정을 보여줍니다. 우리 방법의 결과물은 단일 잠재 $z$, DDIM 인버전의 결과물과 유사합니다. 유의할 점은, 초기 추정 $z^0_t$가 최종 출력으로 간주되는 우리 체계에서 DDIM이 유일한 경우라는 것입니다. 아래에서 보여주듯이, 이 방법은 최소한의 실행 시간 오버헤드로 이미지의 재구성 측면에서 PSNR이 향상되었습니다.

우리 방법의 장점은 인버전 과정만을 수정하고 디퓨전 모델의 전진 과정은 변경하지 않는다는 것입니다. 이는 우리의 방법을 모든 디퓨전 모델에 매우 쉽게 통합할 수 있게 합니다. 또한, 이는 재구성(전진) 과정이 DDIM 기본 과정만큼 빠르게 유지됨을 보장합니다.

더 정교한 방법으로 암시적 함수를 해결하기 위한 뉴턴-랩슨과 공액 그래디언트 같은 방법이 알려져 있습니다. 하지만 이 경우, 고차원의 시드 공간 때문에 또는 수렴하는 데 더 많은 시간이 필요하기 때문에 실용적이지 않다고 판단했습니다. 결과적으로, 몇 번의 반복만으로도 정확한 해를 얻을 수 있는 더 간단한 접근법을 선택했습니다. 추가 세부 사항은 부록 자료에서 찾을 수 있습니다.

수렴

개인적으로 이 논문에서 제일 중요한 부분이라고 생각한다. DDIM inversion에서 원래 매 스텝마다 에러가 도입되던 것을, $z_{t-1}$에 대한 implicit function으로 바꿔서 fixed point iteration으로 멋지게 풀어낸 것은 알겠는데 그게 수렴이 보장되나? 아래 그림처럼 특정 조건을 만족하지 않으면 수렴하지 않는 것으로 아는데.. 

왼쪽: 고정점 반복이 수렴하는 경우. 오른쪽: 고정점 반복이 수렴하지 않는 경우

 

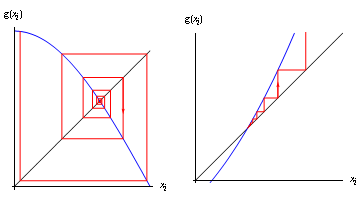
라는 질문에 대한 답을 '경험적으로 그렇다'고 답하는 부분이다. 50개 이미지에 대해 모두 수렴했다고 한다. 왜 그럴까? WGAN처럼 립시츠 제약을 명시적으로 걸어준 것도 아닌데, 뉴럴넷의 weight가 기본적으로 작아서 조건을 만족한 걸까? 아니면 시작 지점을 DDIM inversion한 점으로 좋은 시작점에서 출발해서 그럴까?

고정점 반복은 관심 영역에서 연산자가 수축적일 경우 수렴이 보장됩니다. 공식적으로, 매핑 $f$가 그 도메인에서 수축적이라는 것은 $\rho < 1$인 $\rho$가 존재하여, 모든 $x, y$에 대해 $\|f(x) - f(y)\| \leq \rho\|x - y\|$가 성립하는 경우를 말합니다. 여기서 $\| \cdot \|$는 어떤 행렬 노름을 나타냅니다. 간단한 결과로, 고정점 반복을 두 번 적용하면, 차이의 수열이 단조롭게 감소합니다: $\|x_2 - x_1\| = \|f(f(x_0)) - f(x_0)\| < \|f(x_0) - x_0\| = \|x_1 - x_0\|$.

그림 3. Fixed-point iteration의 수렴 여부 실험적으로 보이기

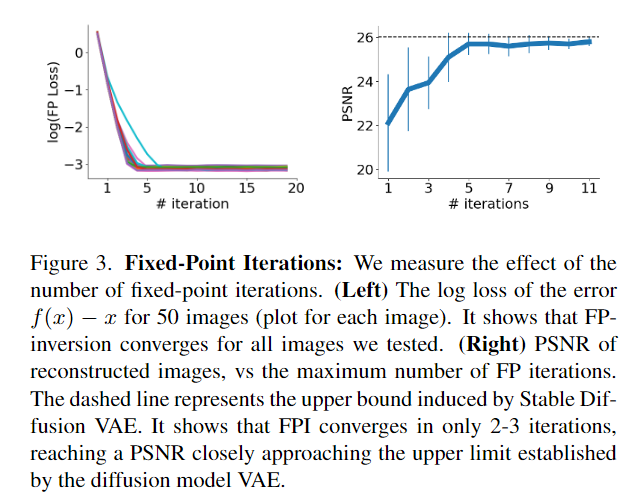
우리의 경우, 함수 $f$가 모든 곳에서 수축적이라는 것은 이론적으로 보장되지 않습니다. 다행히도, 매핑은 우리의 관심 영역에서 여전히 수축적일 수 있습니다. 실제로, 식 (6)을 반복하면 차이 $\Delta z = z^i_t - f(z^i_t)$ (방정식의 잔차)가 반복에 따라 줄어드는 것을 발견했습니다. 그림 3(왼쪽)은 단일 확산 단계에서의 반복 횟수에 따른 FPI 손실(잔차) 곡선을 보여줍니다. 그림 3(오른쪽)은 이미지 재구성에 대한 실행 반복 횟수의 영향을 PSNR 측면에서 묘사합니다. 이 그림들은 FPI가 단 2-3회의 반복으로만 수렴하며, 디퓨전 모델 VAE에 의해 설정된 상한에 가까운 PSNR을 달성한다는 것을 보여줍니다.

 

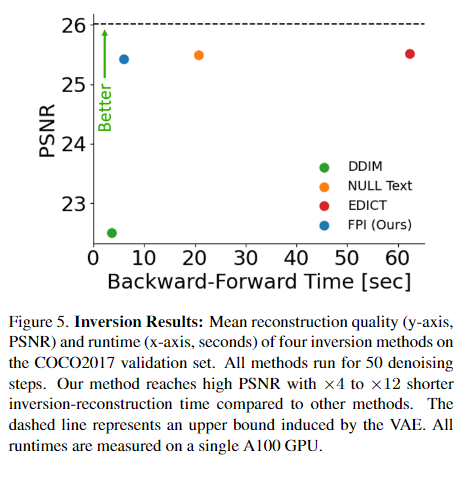
나머지 부분은 인버전이 EDICT, Null-text inversion보다 잘 된다는 내용이니 그냥 읽어보면 어렵지 않게 이해할 수 있을 것이다.

에디팅도 잘 된다고 한다.

 

DDIM 인버전과 fixed-point iteration에 대해 정확히 이해하지 못하고 있었는데 이 논문을 통해 잘 이해하게 되었다. 이렇게 간단한 아이디어로 inversion 시 근사로 에러가 도입되는 문제를 멋지게 푼 정말 훌륭한 논문인 것 같다. 왜 이를 진작 생각하지 못했지? 앞으로는 근사 전에 implicit function 꼴로 나타낼 수 있는지 생각해봐야 할듯..